Cold Open

A few years ago I came across a short paper that I desperately wanted to understand. The magnificent title was “An Option Value Problem from Seinfeld” and the author, Professor Avinash Dixit (of Dixit-Stiglitz model fame), therein discussed methods of solving for “sponge-worthiness.” I don’t think I need to explain why I was immediately drawn to an academic article that focuses on Elaine Benes, but for those of you who didn’t learn about the realities of birth control from this episode of 1990’s television, allow me to briefly explain the relevant Seinfeld-ism.

The character Elaine Benes loyally uses the Today sponge as her preferred form of contraception. However, one day it is taken off the market and, after trekking all over Manhattan, our heroine manages to find only one case of 60 sponges to purchase. The finite supply of sponges poses a daunting question to Elaine… namely, when should she choose to use a sponge? I.e., when is a given potential partner “sponge-worthy”?

JERRY: I thought you said it was imminent.

ELAINE: Yeah, it was, but then I just couldn’t decide if he was really sponge-worthy.

JERRY: “Sponge-worthy”?

ELAINE: Yeah, Jerry, I have to conserve these sponges.

JERRY: But you like this guy, isn’t that what the sponges are for?

ELAINE: Yes, yes - before they went off the market. But I mean, now I’ve got to re-evaluate my whole screening process. I can’t afford to waste any of ’em.

– The Sponge (Seinfeld Season 7 Episode 9)

As an undergraduate reading Professor Dixit’s introduction, I felt supremely excited that an academic article was going to delve into the decision-making processes of one of my favorite fictional characters. However, the last sentence in the introduction gave me pause: “Stochastic dynamic programming methods must be used.” Dynamic programming?? Suffice it to say that I did not grasp the methodological context or mathematical machinery embedded in the short and sweet paper. After a few read-throughs, I filed wispy memories of the paper away in some cluttered corner of my mind… Maybe one day this will make more sense to me…

Flash forward to August 2016. Professor David Laibson, the economics department chair, explains to us fresh-faced G1’s (first-year PhD’s) that he will be teaching us the first part of the macroeconomics sequence… Dynamic Programming. After a few days of talking about Bellman equations, I started to feel as if I had seen related work in some past life. Without all the eeriness of a Westworld-esque robot, I finally remembered the specifics of Professor Dixit’s paper and decided to revisit it with Professor Laibson’s lectures in mind. Accordingly, my goal here is to explain the simplified model set-up of the aforementioned paper and illustrate how basics from dynamic programming can be used in “solving for spongeworthiness.”

Act One: The Model

Dynamic programming refers to taking a complex optimization problem and splitting it up into simpler recursive sub-problems. Consider Elaine’s decision as to when to use a sponge. We can model this as an optimal stopping problem – ie, when should Elaine use the sponge and thus give up the option value of holding it into the future? The answer lies in the solution to a mathematical object called the Bellman equation, which will represent Elaine’s expected present value of her utility recursively.

Using a simplified version of the framework from Dixit (2011), we can explain the intuition behind setting up and solving a Bellman equation. First, let’s lay out the modeling framework. For the sake of computational simplicity, assume Elaine managed to acquire only one sponge rather than the case of 60.¹ With that one glorious sponge in her back pocket, Elaine goes about her life meeting potential partners, and yada yada yada… To make the yada yada’s explicit, we say Elaine lives infinitely and meets one new potential partner every day $t$ who is of some quality $Q_t$. Elaine is not living a regular continuous-time life, instead she gets one romantic option each time period. This sets up the problem in discrete-time since Elaine’s decisions are day-by-day rather than infinitesimally-small-moment-by-infinitesimally-small-moment. If we want to base this assumption somewhat in reality, we could think of Elaine as using Coffee Meets Bagel, a dating app that yields one match per day. I.e., one “bagel” each day.

Dixit interprets an individual’s quality as the utility Elaine receives from sleeping with said person. Now, in reality, Elaine would only be able to make some uncertain prediction of a person’s quality based on potentially noisy signals. The corresponding certainty equivalent (the true quality metric) would be realized after Elaine slept with the person. In other words, there would be a distinction between ex post and ex ante quality assessments—you could even think of a potential partner as an experience good in this sense. (Sorry to objectify you, Scott Patterson.) But, to simplify our discussion, we assume that true quality is observable to Elaine—she knows exactly how much utility she will gain if she chooses to sleep with the potential partner of the day. In defense of that assumption, she does vet potential partners pretty thoroughly.

Dixit also assumes quality is drawn from a uniform distribution over $[0,1]$ and that Elaine discounts the future exponentially by a factor of $\delta$ in the interval $(0,1)$. Discounting is a necessary tool for agent optimization problems since preferences are time dependent. Consider the following set-up for illustrative purposes: Say Elaine gains $X$ utils from eating a box of jujyfruit fruit today, then using our previously defined discount factor, she would gain $δX$ from eating the box tomorrow, $δ^2X$ from eating it the day after tomorrow, and so on.

In general, she gains $δ^nX$ utils from consuming it $n$ days into the future – thus the terminology “exponential discounting.” Given the domain for $δ$, we know unambiguously that $X > δX >δ^2X>...$ and on. That is, if the box of candy doesn’t change between periods (it is always $X$), (assuming it yields positive utility – which clearly it must given questionable related life decisions) Elaine will prefer to consume it in the current time period. I.e., why wait if there is no gain from waiting?

On the other hand, if Elaine wants to drink a bottle of wine today that yields $Y$ utils, but the wine improves by a factor of $w>1$ each day, then whether she prefers to drink it today or tomorrow depends on whether Y – the present utility gain of the current state of the wine—or $δ(wY)$ – the discounted utility gain of the aged (improved) wine—is greater. (I.e., if $δw>1$, she’ll wait for tomorrow.) If Elaine also considers up until $n$ days into the future, she will be comparing, $Y, δ(wY),δ^2X(w^2Y), ...,$ and $δ^n(w^nY)$.

In our set-up Elaine receives some quality offer each day that is neither static (as in the jujyfruit fruit example) nor deterministically growing (as in the wine example), rather the quality is drawn from a defined distribution (the uniform distribution on the unit interval – mainly chosen to allow for straightforward computations). While quality is observable in the current period, the future draws are not observable, meaning that Elaine must compare her current draw with an expectation of future draws.

In short, everyday Elaine has the choice whether to use the sponge and gain $Q_t$ through her utility function, or hold the sponge for a potentially superior partner in the future. In other words, Elaine’s current value function is expressed as a choice between the “flow payoff” $Q_t$ and the discounted “continuation value function.” Since she is utility maximizing, she will always choose the higher of these two options. Again, since the continuation value function is uncertain, as future quality draws are from some distribution, we must use the expectation operator in that piece of the maximization problem. Elaine’s value function is thus:

$$V(Q_t)=max\{Q_t,\delta EV(Q_{t+1})\} $$

This is the Bellman equation of lore! It illustrates a recursive relationship between the value functions for different time periods, and formalizes Elaine’s decision as a simple optimal stopping problem.

Act Two: Solving for Sponge-worthiness

To solve for sponge-worthiness, we need to find the value function that solves the Bellman equation, and derive the associated optimal policy rule. Our optimal policy rule is a function that maps each point in the state space (the space of possible quality draws) to the action space such that Elaine achieves payoff $V(Q_t)$ for all feasible quality draws in $[0,1]$. The distribution of $Q_{t+1}$ are stationary and independent of $Q_t$, as the draws are perpetually from $U[0,1]$.² Due to the aforementioned stationarity and independence, the value of holding onto the sponge $δEV(Q_{t+1})$ is constant for all days.

By this logic, if a potential partner of quality $Q'$ is sponge-worthy, then $Q'≥δEV(Q_{t+1})$! Note that for all $Q''>Q',Q''>δEV(Q_{t+1})$, so some partner of quality $Q''$ must also be considered sponge-worthy. Similarly, if a person of quality $Q'$ is not sponge-worthy, then $δEV(Q_{t+1}) ≥ Q'$ and for all $Q''<Q', Q''<δEV(Q_{t+1})$, so any partner of quality $Q''$ must also not be sponge-worthy. Thus, the functional form of the value function is:

$$ V(Q_t)=\begin{cases} Q_t & \text{if } Q_t > Q^*\\ Q^*& \text{if } Q_t \leq Q^* \end{cases} $$

In other words, our solution will be a threshold rule where the optimal policy is to use the sponge if $Q_t > Q^*$ and hold onto the sponge otherwise. The free parameter we need to solve for is $Q^*$, which we can conceptualize as the all-powerful quality level that separates`the sponge-worthy from the not!

Act Three: What is $Q^*$?

When $Q_t= Q^*$, Elaine should be indifferent between using the sponge and holding onto it. This means that the two arguments in the maximization should be equal – that is, the flow payoff $Q*$ and the discounted continuation value function $δEV(Q_{t+1})$. We can thus set $Q^*=δEV(Q_{t+1})$ and exploit the fact that we defined $Q \sim U[0,1]$, to make the following calculations:

$$Q^*=\delta EV(Q_{t+1})$$ $$Q^*=\delta (\int_{0}^{Q^*} Q^* d Q_{t+1}+\int_{Q^*}^{1} Q_{t+1} d Q_{t+1} )$$ $$Q^*=\delta ([Q^*Q_{t+1}] \Big|_0^{Q^*} + [\frac{(Q_{t+1})^2}{2}] \Big|_{Q^*}^{1}) $$ $$Q^*=\delta (\frac {{Q^*}^2}{2} +\frac{1}{2}) $$ $$\frac{\delta {Q^*}^2}{2}-Q^*+\frac{\delta}{2}=0$$ $$Q^*=\frac{1}{\delta} \pm \sqrt{\frac{1}{\delta^2} -1}$$

The positive root yields a $Q^*>1$, which would mean that Elaine never uses the sponge. This cannot be the optimal policy, so we eliminate this root. In effect, we end up with the following solution for $Q^*$:

$$Q^*=\frac{1}{\delta}-\sqrt{\frac{1}{\delta^2} -1}$$

Given this $Q^*$, it is optimal to use the sponge if $Q_t> Q^*$, and it is optimal to hold the sponge $Q^*≥Q_t$. Thus, as is required by the definition of optimal policy, for all values of $Q_t$:

$$V(Q_t)=max\{Q_t, Q^*\}=max\{Q_t, \delta EV(Q_{t+1}) \}$$

We can interpret the way the $Q*$ threshold changes with the discount factor $δ$ using basic economic intuition. As $δ$ approaches $1$ (Elaine approaches peak patience), $Q^*$ then approaches 1, meaning Elaine will accept no partner but the one of best possible quality. At the other extreme, as $δ$ approaches $0$ (Elaine approaches peak impatience), $Q*$ then approaches $0$, meaning Elaine will immediately use the sponge with the first potential partner she meets.

To make this visually explicit, let’s use a graph to illustrate Elaine’s value function for some set $δ$. Take $δ=0.8$, then $Q^*=0.5$, a clear-cut solution for the sponge-worthiness threshold. Given these numbers, the relationship between the value function and quality level can be drawn out as such:

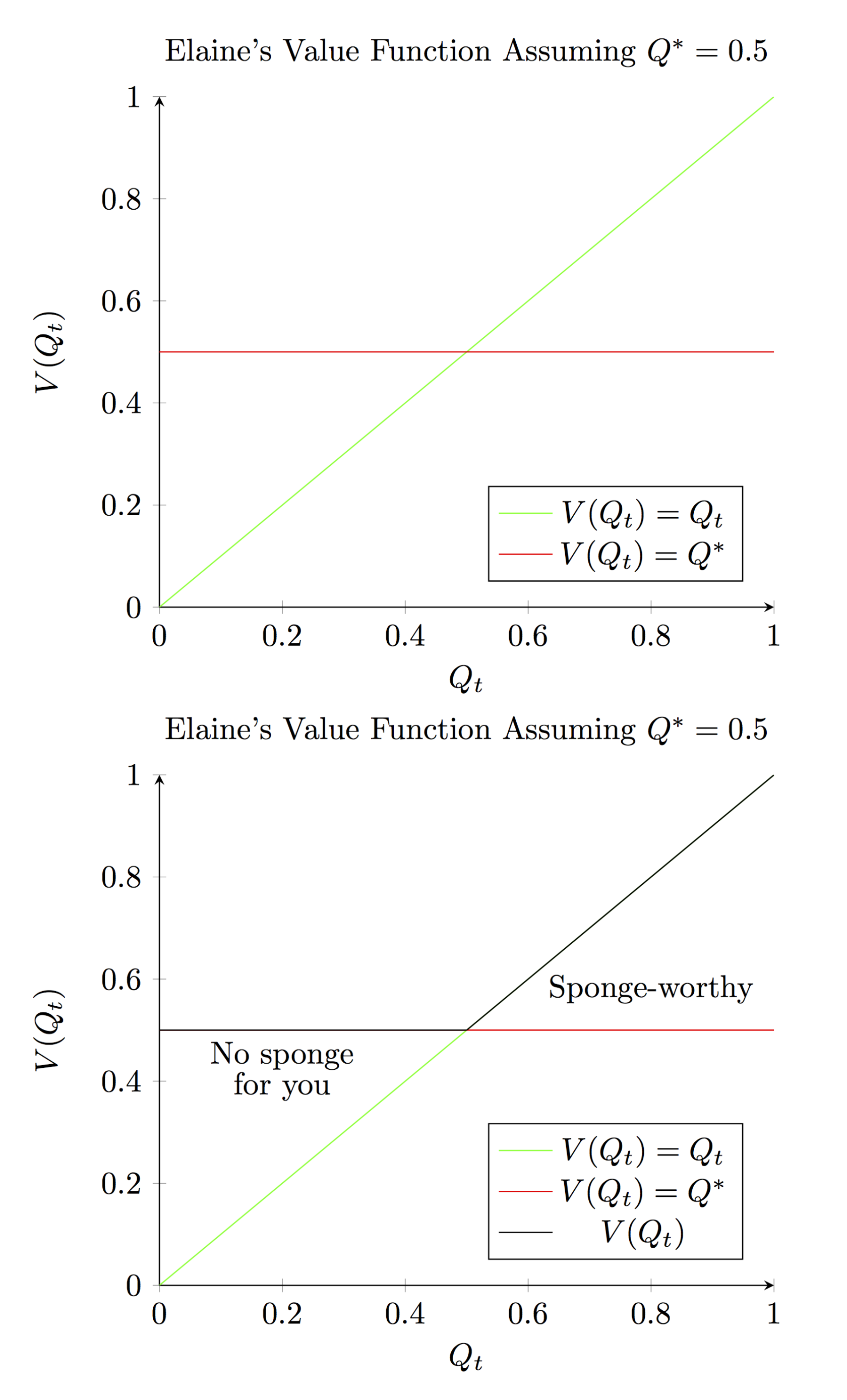
The first diagram illustrates the two pieces that make up Elaine’s value function, while the second then uses the black line to denote the value function, as the value function takes on the maximum value across the space of quality draws. Whether the value function conforms to the red or green line hinges on whether we are in the sponge-worthy range or not. As explained earlier, before the sponge-worthiness threshold, the option value of holding the sponge is the constant such that $Q^*=δEV(Q_{t+1})$. After hitting the magical point of sponge-worthiness, the value function moves one-for-one with $Q_t$.

Note that alternative choices for the discount rate would yield different $Q^*$’s, which would shift the red line up or down depending on the value, which in turn impact the leftmost piece of the value function in the second graph. These illustrations are very similar to diagrams we drew in Professor Laibson’s module, but with some more advanced technical graph labelings than what we were exposed to in class (i.e., “no sponge for you” and “sponge-worthy”).

Act Four: Extensions

In our set-up, the dependence of the value function is simple since there is one sponge and Elaine is infinitely lived. However, it could be that we solve for a value function with more complex time and resource dependence. This could yield a more realistic solution that takes into account Elaine’s age and mortality and the 60 sponges in the valuable case of contraception. We could even perform the sponge-worthiness calculations for Elaine’s monotonically increasing string of sponge quantity requests: 3, 10, 20, 25, 60! (These numbers based in the Seinfeld canon clearly should have been in the tabular calculations performed by Dixit.)

For computational purposes, we also assumed that quality is drawn independently each period (day) from a uniform distribution on the unit interval. (Recall that a uniform distribution over some interval means that each value in the interval has equal probability.) We could alternatively consider a normal distribution, which would likely do a better job of approximating the population quality in reality. Moreover, the quality of partners could be drawn from a distribution whose bounds deterministically grow over time, as there could be an underlying trend upward in the quality of people Elaine is meeting. Perhaps Coffee Meets Bagel gets better at matching Elaine with bagels, as it learns about her preferences.

Alternatively, we could try and legitimize a more specific choice of a distribution using proper Seinfeld canon. In particular, Season 7 Episode 11 (“The Wink,” which is just 2 episodes after “The Sponge”) makes explicit that Elaine believes about 25% of the population is good looking. If we assume Elaine gains utility only from sleeping with good looking people, we could defend using a distribution such that 75% of quality draws are exactly 0 and the remaining 25% of draws are from a normal distribution ranging from 0 to 1.³

Regardless of the specific distribution or time/resource constraint choices, the key take-away here is the undeniably natural formulation of this episode’s plot line as an optimal stopping problem. Throughout the course of our six weeks with Professor Laibson, our class used dynamic programming to approach questions of growth, search, consumption, and asset pricing… while these applications are diverse and wide-ranging, don’t methods seem even more powerful when analyzing fictional romantic encounters!?

Recap

See here for a quick recap of how to solve the problem outlined in this post.

References

As explained earlier, this write-up is primarily focused on the aforementioned Dixit (2011) paper, but also draws on materials from Harvard’s Economics 2010D sequence. In particular, “Economics 2010c: Lecture 1 Introduction to Dynamic Programming” by David Laibson (9/1/2016) & “ECON 2010c Section 1” by Argyris Tsiaras (9/2/2016).